- Django Interview Questions
- Python Array Examples
- Python enum
- Python Enumerate with Example
- Python Flask Tutorial For Beginners
- Python For Beginners - Way To Success
- Python For Data Science Tutorial For Beginners
- Python for loop
- Python GET and POST Requests
- Python IDEs for Python Programmers
- Python Interview Questions
- Python Lists with Examples
- Python Partial Function Using Functools
- Python Print
- How to generate random numbers in python
- Python Regular Expression (RegEx) Cheatsheet
- Python Sleep Method
- Python List Methods
- Python Split Method with Example
- Python String Functions
- Python Tutorial
- Python Variable Types
- Python vs Java
- Python vs SAS vs R
- Python Operators
- Code Introspection in Python
- Comprehensions in Python
- Python Exception Handling
- Defining Functions - Python
- Generators & Iterators in python
- Install Python on Windows and Linux
- Introduction to Python Programming
- Lists concepts in Python
- Loops in Python
- Regular Expression Operations in Python
- Python Serialization
- String Formatting - Python
- R vs Python: Which is better R or Python?
- Six Digit Salary With Python
- Top 20 Python Frameworks List
- Why Learn Python
- Python Substring
- OOPs Interview Questions
- Career Shift To Python : Success Guaranteed
- Face Recognition with Python
- Go vs Python
- Pyspark Interview Questions
- Python Pandas Interview Questions
- OpenCV Interview Questions
- Python Project Ideas
- Flask Interview Questions and Answers
- Array Interview Questions
- What is PyCharm?
- What is Seaborn in Python?
- What is Anaconda Navigator
- Python Data Science Interview Questions
- Genpact Interview Questions
- Python Developer Job Description
- Pandas Projects and Use Cases
- DataFrame Tutorial
- How to install Python on Windows
- Pyspark DataFrame
Arrays with different sizes cannot perform any arithmetic operations like addition, subtraction, etc. To overcome this, we duplicate the smaller array to have the same dimensions and size as the larger one. This method is called array broadcasting, and is available in Numpy to perform array arithmetic operations to simplify the code.
In this article, we’ll discuss the basics of array broadcasting and how to implement broadcasting with NumPy.
| Broadcasting in NumPy: Table of Content |
Introduction to NumPy Broadcasting
Broadcasting is the term used to describe how NumPy manages arrays in various shapes while carrying out arithmetic operations. To ensure that their shapes are identical, the smaller array is "broadcast" over the larger array with some limitations. Broadcasting makes it possible to use looping by vectorizing array operations. It accomplishes this without pointless data duplication and frequently results in the development of effective methods. However, broadcasting can occasionally be a mistake because it results in inefficient memory usage, which slows computation.
NumPy operations are typically executed element-by-element on pairs of arrays. The two arrays must, in the most straightforward scenario, have exactly the same shape, as shown in the illustration below:
| If you would like to become a Python-certified professional, then visit Mindmajix - A Global online training platform for “Python Training” Course. This course will help you to achieve excellence in this |
An Example will help you understand better
Assume that each datum in our huge data set contains a list of parameters. The data collection size is determined by the number of rows in the 2-D array we have in Numpy, where each row is a datum. If we want to scale all of these data, each parameter would have its own scaling factor, or we could say that each parameter is multiplied by a certain amount.
Let's use a macronutrient breakdown to calculate the number of calories in various foods so that everything is obvious. In general, lipids (9 calories per gramme), protein (4 cpg), and carbohydrates make up the caloric components of diet (4 cpg). If we list some foods (our data) and list the macronutrient breakdown for each food, We can scale every nutrient by its caloric value to determine each food item's caloric breakdown.
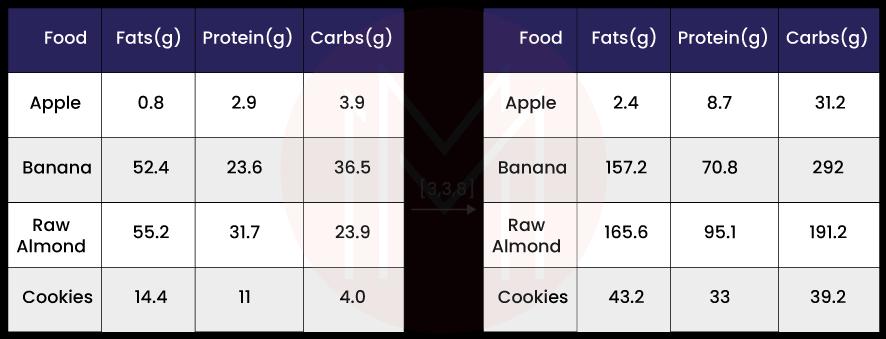
We can now compute all kinds of helpful information thanks to this change. For instance, how many calories are there in total in a certain food or, given a breakdown of my dinner, how many calories were from protein, and so on.
Rules for Numpy Broadcasting
NumPy analyzes two arrays' shapes element-by-element when performing an operation. It moves leftward, starting with the trailing (or rightmost) dimensions. When two dimensions coexist,
- No matter if they are equivalent
- One of them is 1.
If these requirements are not met, the arrays are considered to have incompatible forms and a ValueError: operands could not be broadcast together exception is raised. The size of the resultant array equals the length of each input axis that is not 1.
Arrays do not have to share the same number of dimensions. For instance, you could multiply the image by a one-dimensional array with three values if you had an array of 256x256x3 with RGB values and wanted to scale each color in the image by a different value. These arrays can be seen to be compatible by aligning the sizes of their trailing axes with the broadcast rules:

The other dimension is used if either of the dimensions being compared is one. In other words, size 1 dimensions are "copied" or stretched to meet size 2 dimensions.
The following illustration shows how during the broadcast operation, the axes with length one in both the A and B arrays are enlarged to a larger size:

Broadcastable arrays
If the aforementioned rules result in an acceptable outcome, a group of arrays is said to be "broadcastable" to the same form.
For instance, if the shapes of a, b, c, and d are (5,1), (1,6), (6), and (), respectively, and d is a scalar, then a, b, c, and d are all broadcastable to dimension (5,6); and:
- Because a[:,0] is broadcast to the other columns, a behaves as a (5,6) array.
- In the sense that b[0,:] is broadcast to the other rows, b behaves as a (5,6) array.
- Finally, because c[:] is broadcast to every row, it behaves like a (1,6) array and hence behaves like a (5,6) array.
- D functions as a single-value repeating array (5,6).
Here are a few more instances:

Related Article: Python Tutorial
Broadcasting example # 1: Single Dimension Array

Output:
[17 11 19]
3
[20 14 22]Broadcasting example # 2: Two-Dimensional Array

Output:
[[11 22 33]
[10 20 30]]
4
[[15 26 37]
[14 24 34]]
Broadcasting example # 3:Three-Dimensional Array

Output:
[[ 4 5]
[ 8 10]
[12 15]]
[[2 4 6]
[5 7 9]]
[[ 5 6 7]
[ 9 10 11]]
[[ 5 6 7]
[ 9 10 11]]
[[ 2 4 6]
[ 8 10 12]]
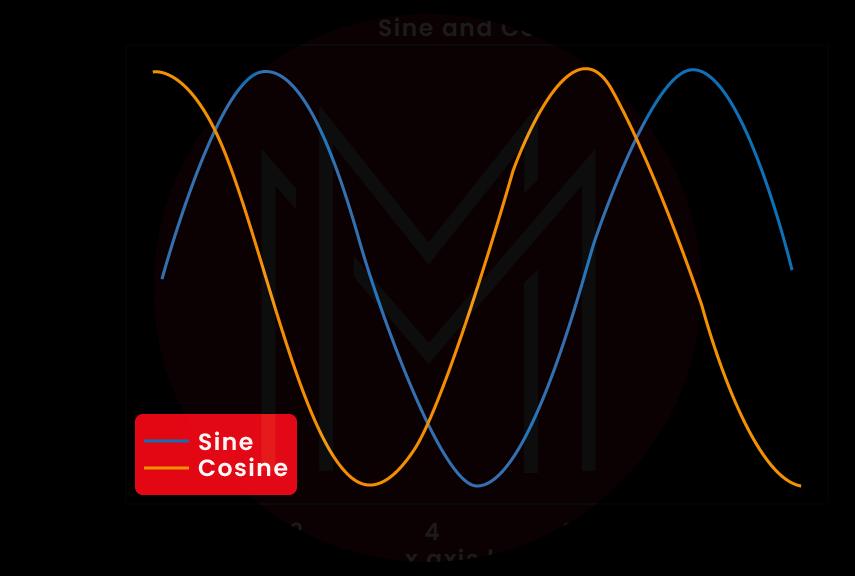
Plotting a two-dimensional function
The display of images based on two-dimensional functions is another common application of broadcasting. If a function z=f needs to be defined.

Output:
Broadcasting in NumPy FAQs
1. What do you mean by broadcasting in Python?
When operations on arrays of different dimensions encounter limitations, the shorter array is broadcast across the larger array, ensuring that their shapes are compatible. This action is referred to as broadcasting.
2. What is a broadcasting operation?
When carrying out operations that produce constraints, Numpy handles arrays of various dimensions in a manner known as "broadcasting."; To ensure that they have similar shapes, the shorter array is distributed across the larger array.
3. What is broadcasting in DataFrame?
The word "broadcasting" essentially describes the output rules that apply when operations are performed on n-dimensional arrays (which could be panels, dataframes, or series) or scalar values.
4. Can you broadcast more than 1 dimension?
Only when all of the arrays' dimensions have the same shape or one has a dimension size of 1 can broadcasting be done.
Conclusion
In this ‘Broadcasting in NumPy’ article, we discussed the basic concepts of NumPy. We explored the various functions of NumPy arrays as well as how to create one. We went through several mathematical operations on NumPy using broadcasting.
If you have any questions, please leave them in the comments below, and our subject matter experts will help you out.
 On-Job Support Service
On-Job Support Service
Online Work Support for your on-job roles.

Our work-support plans provide precise options as per your project tasks. Whether you are a newbie or an experienced professional seeking assistance in completing project tasks, we are here with the following plans to meet your custom needs:
- Pay Per Hour
- Pay Per Week
- Monthly
| Name | Dates | |
|---|---|---|
| Python Training | Feb 24 to Mar 11 | View Details |
| Python Training | Feb 28 to Mar 15 | View Details |
| Python Training | Mar 03 to Mar 18 | View Details |
| Python Training | Mar 07 to Mar 22 | View Details |

Madhuri is a Senior Content Creator at MindMajix. She has written about a range of different topics on various technologies, which include, Splunk, Tensorflow, Selenium, and CEH. She spends most of her time researching on technology, and startups. Connect with her via LinkedIn and Twitter .
















